Constante de Euler-Mascheroni

La constante de Euler-Mascheroni (también conocida como constante de Euler) es una constante matemática que aparece principalmente en teoría de números, y se denota con la letra griega minúscula γ (Gamma).
Se define como el límite de la diferencia entre la serie armónica y el logaritmo natural:

$\gamma = \lim_{n \rightarrow \infty } \left[ \sum_{k=1}^n \frac{1}{k} - \ln(n)\right]=\int_1^\infty\left({1\over\lfloor x\rfloor}-{1\over x}\right)\,dx$

Su valor aproximado es:

$\gamma \approx 0,577\;215\;664\;901\;532\;860\;606\;\ldots$

No debe confundirse con el número e, también llamado número de Euler.

Historia

La constante apareció por primera vez en 1734, en un artículo escrito por el matemático suizo Leonhard Euler, llamado De Progressionibus harmonicis observationes, calculando los 6 primeros dígitos para la constante y llamándola C. En 1781 calcularía otros 10 decimales más. En 1790, Lorenzo Mascheroni calcularía los primeros 19 decimales y la denotaría como A. Ya más tarde se denotaría de la forma moderna como γ, debido a su conexión con la función gamma.^[1]

Propiedades

El número γ no se ha probado que sea algebraico o transcendente, de hecho, ni siquiera se conoce si γ es irracional o no^[2] . El análisis de fracciones continuas revela, que de ser racional, su denominador debe ser muy elevado ( actualmente del orden de 10²⁴²⁰⁸⁰).^[3] Debido a que está presente en un gran número de ecuaciones y relaciones, la racionalidad o irracionalidad de γ está entre los problemas abiertos más importantes de matemáticas.
A continuación se exponen las más importantes relaciones de γ con funciones, series e integrales.

Representación original (Euler)

Descubierta en 1734 por Euler, representándola como una serie infinita de la siguiente forma:

$\gamma = \sum_{k=1}^\infty \left[ \frac{1}{k} - \ln \left( 1 + \frac{1}{k} \right) \right]$

Relación con la función Gamma

Si tomamos la función gamma, la derivamos y evaluamos en 1, obtenemos -γ. Lo mismo pasa si evaluamos la función digamma en 1, o sea:

$-\gamma = {\Gamma}'(1) = \Psi(1) \,\!$

también como el límite:

$\gamma = \lim_{n \to \infty} \left [ n - \Gamma \left ( \frac{1}{n} \right ) \right ]$

El límite relacionado con la función beta (expresada en términos de función gamma) es:

$-\gamma = \lim_{n \to \infty} \left [ \frac{ \Gamma(\frac{1}{n}) \Gamma(n+1)\, n^{1+{1 \over n}}}{\Gamma(2+n+\frac{1}{n})} - \frac{n^2}{n+1} \right ]$

y como función beta:

$-\gamma = \lim_{n \to \infty} \left [n^{2+{1 \over n}} \, \Beta \left( 1 + \frac{1}{n},\, n + 1 \right ) - \frac{n^2}{n+1} \right ]$

Relación con la función Zeta de Riemann

γ se puede expresar como suma infinita, cuyos términos invocan la función zeta de Riemann para números positivos de la siguiente forma:

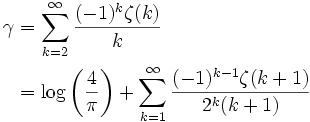
$\begin{align} \gamma & = \sum_{k=2}^{\infty} \frac{(-1)^k\zeta(k)}{k} \\ {} & = \log \left ( \frac{4}{\pi} \right ) + \sum_{k=1}^{\infty} \frac{(-1)^{k-1} \zeta(k+1)}{2^k (k+1)} \end{align}$

Otras series relacionadas con la función zeta son:

$\begin{align} \gamma & = \frac{3}{2}- \log 2 - \sum_{k=2}^\infty (-1)^k\,\frac{k-1}{k} [\zeta(k)-1]\\ {} & = \lim_{n \to \infty} \left [ \frac{2\,n-1}{2\,n} - \log\,n + \sum_{k=2}^n \left ( \frac{1}{k} - \frac{\zeta(1-k)}{n^k} \right ) \right ]\\ {} & = \lim_{n \to \infty} \left [ \frac{2^n}{e^{2^n}} \sum_{k=0}^\infty \frac{2^{k \,n}}{(k+1)!} \sum_{t=0}^k \frac{1}{t+1} - n\, \log 2+ \mathcal{O} \left ( \frac{1}{2^n\,e^{2^n}} \right ) \right ] \end{align}$

El término error de la última serie decrece exponencialmente en función de n. Como resultado, la fórmula resulta muy eficiente para calcular grandes cantidades de dígitos de la constante con gran precisión.

Otros interesantes límite relacionado con la constante de Euler-Mascheroni y la función zeta es el límite antisimétrico (Sondow, 1998)

$\gamma = \lim_{s \to 1^+} \sum_{n=1}^\infty \left ( \frac{1}{n^s}-\frac{1}{s^n} \right ) = \lim_{s \to 1} \left ( \zeta(s) - \frac{1}{s-1} \right )$

Representación con integrales

γ es igual al valor de un número determinado de integrales definidas:

$\begin{align} \gamma & = - \int_0^\infty { e^{-x} \log x }\,dx \\ {} & = - \int_0^1 { \log\log\left (\frac{1}{x}\right ) }\,dx \\ {} & = \int_0^\infty {\left (\frac{1}{1-e^{-x}}-\frac{1}{x} \right )e^{-x} }\,dx \\ {} & = \int_0^\infty { \frac{1}{x} \left ( \frac{1}{1+x}-e^{-x} \right ) }\,dx \\ \end{align}$