Constante de Euler-Mascheroni
La constante de Euler-Mascheroni (también conocida como constante de Euler) es una constante matemática que aparece principalmente en teoría de números, y se denota con la letra griega minúscula γ (Gamma).
Se define como el límite de la diferencia entre la serie armónica y el logaritmo natural:
Su valor aproximado es:
A continuación se exponen las más importantes relaciones de γ con funciones, series e integrales.
Otros interesantes límite relacionado con la constante de Euler-Mascheroni y la función zeta es el límite antisimétrico (Sondow, 1998)
Se define como el límite de la diferencia entre la serie armónica y el logaritmo natural:
![\gamma = \lim_{n \rightarrow \infty } \left[
\sum_{k=1}^n \frac{1}{k} - \ln(n)\right]=\int_1^\infty\left({1\over\lfloor x\rfloor}-{1\over x}\right)\,dx](http://upload.wikimedia.org/math/1/0/5/1052749ba2986f314a37315f1e0e6507.png)
Historia
La constante apareció por primera vez en 1734, en un artículo escrito por el matemático suizo Leonhard Euler, llamado De Progressionibus harmonicis observationes, calculando los 6 primeros dígitos para la constante y llamándola C. En 1781 calcularía otros 10 decimales más. En 1790, Lorenzo Mascheroni calcularía los primeros 19 decimales y la denotaría como A. Ya más tarde se denotaría de la forma moderna como γ, debido a su conexión con la función gamma.[1]Propiedades
El número γ no se ha probado que sea algebraico o transcendente, de hecho, ni siquiera se conoce si γ es irracional o no[2] . El análisis de fracciones continuas revela, que de ser racional, su denominador debe ser muy elevado ( actualmente del orden de 10242080).[3] Debido a que está presente en un gran número de ecuaciones y relaciones, la racionalidad o irracionalidad de γ está entre los problemas abiertos más importantes de matemáticas.A continuación se exponen las más importantes relaciones de γ con funciones, series e integrales.
Representación original (Euler)
Descubierta en 1734 por Euler, representándola como una serie infinita de la siguiente forma:![\gamma = \sum_{k=1}^\infty \left[ \frac{1}{k} - \ln \left( 1 + \frac{1}{k} \right) \right]](http://upload.wikimedia.org/math/8/9/2/89211028b40ce9518421d03a40474722.png)
Relación con la función Gamma
Si tomamos la función gamma, la derivamos y evaluamos en 1, obtenemos -γ. Lo mismo pasa si evaluamos la función digamma en 1, o sea:
![\gamma = \lim_{n \to \infty} \left [ n - \Gamma \left ( \frac{1}{n} \right ) \right ]](http://upload.wikimedia.org/math/9/c/6/9c638e815f0b7097504a14c3b11b8242.png)
![-\gamma = \lim_{n \to \infty} \left [ \frac{ \Gamma(\frac{1}{n}) \Gamma(n+1)\, n^{1+{1 \over n}}}{\Gamma(2+n+\frac{1}{n})} - \frac{n^2}{n+1} \right ]](http://upload.wikimedia.org/math/5/6/6/566f6e07cfe5a5d190a810ac464d9745.png)
![-\gamma = \lim_{n \to \infty} \left [n^{2+{1 \over n}} \, \Beta \left( 1 + \frac{1}{n},\, n + 1 \right ) - \frac{n^2}{n+1} \right ]](http://upload.wikimedia.org/math/7/e/3/7e31a0734e46433412820fdc04d4d120.png)
Relación con la función Zeta de Riemann
γ se puede expresar como suma infinita, cuyos términos invocan la función zeta de Riemann para números positivos de la siguiente forma:
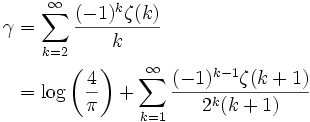
![\begin{align}
\gamma & = \frac{3}{2}- \log 2 - \sum_{k=2}^\infty (-1)^k\,\frac{k-1}{k} [\zeta(k)-1]\\
{} & = \lim_{n \to \infty} \left [ \frac{2\,n-1}{2\,n} - \log\,n + \sum_{k=2}^n \left ( \frac{1}{k} - \frac{\zeta(1-k)}{n^k} \right ) \right ]\\
{} & = \lim_{n \to \infty} \left [ \frac{2^n}{e^{2^n}} \sum_{k=0}^\infty \frac{2^{k \,n}}{(k+1)!} \sum_{t=0}^k \frac{1}{t+1} - n\, \log 2+ \mathcal{O} \left ( \frac{1}{2^n\,e^{2^n}} \right ) \right ]
\end{align}](http://upload.wikimedia.org/math/5/d/2/5d210739d9779cf0ca8f4658c6dd15ef.png)
Otros interesantes límite relacionado con la constante de Euler-Mascheroni y la función zeta es el límite antisimétrico (Sondow, 1998)
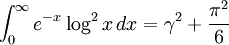
, donde 1 representa proporcionalmente a la mitad de la base, la raíz cuadrada del número áureo a la altura hasta el vértice inexistente y el número áureo o hipotenusa del triángulo a la apotema de la Gran Pirámide. Esta tesis ha sido defendida por los matemáticos Jarolimek, K. Kleppisch y W. A. Price (ver referencias), cuenta con el testimonio histórico de Herodoto y resulta teóricamente con sentido, aunque una construcción de semejante tamaño deba contener errores inevitables a toda obra arquitectónica y a la misma naturaleza de la tecnología humana, que en la práctica puede manejar únicamente números racionales. Los demás investigadores famosos se inclinan por la hipótesis de que los constructores intentaron una cuadratura del círculo, pues la raíz cuadrada del número áureo se aproxima mucho al cociente de 4 sobre p. Pero una construcción tal, aunque se conociera p con una aproximación grande, carecería completamente de sentido matemático. No obstante, en base a mediciones no es posible elegir entre una u otra pues la diferencia sobre el monumento real no es mayor a 14,2 cm y esta pequeña variación queda enmascarada por las incertidumbres de las medidas, los errores constructivos y, principalmente, porque la pirámide perdió el revestimiento en manos de los primeros constructores de El Cairo. Para que esto quede más claro, una precisión del 1 por mil en una base de 230 metros equivale a 23 centímetros y en la altura está en el orden de la diferencia real que debería existir entre ambas posibilidades. 
. Por medio de cuatro diagonales suministra las principales proporciones verticales y horizontales. Este rectángulo es descompuesto en seis de módulo 
y cuatro cuadrados. Como dato adicional para indicar la complejidad del tratamiento del edificio se tiene que en 1837 fueron descubiertas correcciones ópticas en el Partenón. El templo tiene tres vistas principales y si sus columnas estuvieran efectivamente a plomo, todas sus líneas fuesen paralelas y perfectamente rectas y los ángulos rectos fueran exactos, por las propiedades de la visión humana el conjunto se vería más ancho arriba que en la base, sus columnas se percibirían inclinadas hacia afuera y la línea que fundamenta el techo sobre las columnas se vería como una especie de catenaria, con los extremos del edificio aparentemente más altos que el centro. Los constructores hicieron la construcción compensando estos efectos de ilusión óptica inclinando o curvando en sentido inverso a los elementos involucrados. Así las columnas exteriores,en ambos lados del frente, están inclinadas hacia adentro en un ángulo de 2,65 segundos de arco, mientras que las que están en el medio tienen una inclinación de 2,61 segundos de arco. La línea que formarían los dinteles entre columnas y que constituye la base del triángulo que corona el edificio, en realidad es un ángulo de 2,64 segundos de arco con el vértice más elevado que los extremos. De esta forma, y con otras correcciones que no se mencionan aquí, se logra que cualquier observador que se sitúe en los tres puntos principales de vista vea todo el conjunto paralelo, uniforme y recto. 
. Este número irracional tiene infinitos decimales, pero la afinación se hace redondeando las cifras de las frecuencias a uno o dos decimales. De cualquier manera, el error tonal total cometido no es superior al doceavo de tono y el oído humano no lo nota. La uniformidad de la separación de las notas y la coincidencia de 
AP, donde A es un punto del semieje positivo de las x y P(x,y), el punto del extremo, se definen las razones trigonométricas del ángulo en la forma:
sen 30º = y/r= (r/2) / r = 1/2
sen 60º= y/r= (r 3½ / 2)/r= 3½ / 2
sen 45º = y/r = 2½ / 2
Teniendo en cuenta la definición de cada razón trigonométrica, se deduce:
Observamos que y'=x y que x'=y
sen 
sen 
cos(
significa que existe un archivo alternativo, 
