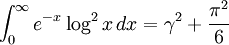triplico: Dia del Logro
Matematica Zona
lunes, 5 de agosto de 2013
martes, 16 de julio de 2013
CONSTANTE DE EULER
Constante de Euler-Mascheroni
La constante de Euler-Mascheroni (también conocida como constante de Euler) es una constante matemática que aparece principalmente en teoría de números, y se denota con la letra griega minúscula γ (Gamma).
Se define como el límite de la diferencia entre la serie armónica y el logaritmo natural:
Su valor aproximado es:
A continuación se exponen las más importantes relaciones de γ con funciones, series e integrales.
Otros interesantes límite relacionado con la constante de Euler-Mascheroni y la función zeta es el límite antisimétrico (Sondow, 1998)
Se define como el límite de la diferencia entre la serie armónica y el logaritmo natural:
Historia
La constante apareció por primera vez en 1734, en un artículo escrito por el matemático suizo Leonhard Euler, llamado De Progressionibus harmonicis observationes, calculando los 6 primeros dígitos para la constante y llamándola C. En 1781 calcularía otros 10 decimales más. En 1790, Lorenzo Mascheroni calcularía los primeros 19 decimales y la denotaría como A. Ya más tarde se denotaría de la forma moderna como γ, debido a su conexión con la función gamma.[1]Propiedades
El número γ no se ha probado que sea algebraico o transcendente, de hecho, ni siquiera se conoce si γ es irracional o no[2] . El análisis de fracciones continuas revela, que de ser racional, su denominador debe ser muy elevado ( actualmente del orden de 10242080).[3] Debido a que está presente en un gran número de ecuaciones y relaciones, la racionalidad o irracionalidad de γ está entre los problemas abiertos más importantes de matemáticas.A continuación se exponen las más importantes relaciones de γ con funciones, series e integrales.
Representación original (Euler)
Descubierta en 1734 por Euler, representándola como una serie infinita de la siguiente forma:Relación con la función Gamma
Si tomamos la función gamma, la derivamos y evaluamos en 1, obtenemos -γ. Lo mismo pasa si evaluamos la función digamma en 1, o sea:Relación con la función Zeta de Riemann
γ se puede expresar como suma infinita, cuyos términos invocan la función zeta de Riemann para números positivos de la siguiente forma:Otros interesantes límite relacionado con la constante de Euler-Mascheroni y la función zeta es el límite antisimétrico (Sondow, 1998)
Representación con integrales
γ es igual al valor de un número determinado de integrales definidas:NEPERIANO
La matemática está llena de fórmulas, teoremas y constantes, las cuales aprendemos pero a veces no comprendemos. Las matemáticas parecieran artificiosas, sin conexión con la realidad. Esto pasa seguido con el logaritmo natural o neperiano, la famosa letra “e” que enseñan en la escuela y que tantos dolores de cabeza suele ocasionar a los estudiantes.
El logaritmo natural o neperiano es uno de esos conceptos que aprendemos sin encontrarle ninguna utilidad práctica más que para los físicos o químicos. La ciencia es excitante, pero las matemáticas detrás de ella pueden frustrarnos. Sin embargo, detrás de cada concepto matemático existe una historia, muchas veces fascinante de cómo una necesidad y una mente creativa pueden encontrar en los números una representación sintetizada de la realidad.
El logaritmo natural, también conocido como logaritmo neperiano en honor del escocés John Napier (cuyo nombre latinizado es Neper) utiliza como base la famosa letra “e” un numero irracional (una división sin fin) cuyo valor aproximado es 2.71821... Los logaritmos pueden ser de cualquier base, sin embargo, los más utilizados es el logaritmo de base 10 también conocido como logaritmo vulgar y el logaritmo natural o neperiano, el cual es más utilizado en ciencias.
Napier fue el creador de la palabra logaritmo (del griego “logos” razón y “arithmos”, numero). Sin embargo, como todo en la ciencia hubo otro hombre quien también trabajó sobre el mismo concepto incluso antes que Napier, este fue el relojero suizo Jobst Bürgi. Sin embargo por cuestión de tiempo, tardó en publicar sus investigaciones hasta el año 1620.
Los logaritmos surgieron por la necesidad de hacer más fáciles operaciones complicadas o tediosas. El concepto de logaritmo como lo conocemos actualmente no surgió de forma inmediata, sino que llevo un proceso de maduración hasta la forma que lo conocemos hoy en día. Se utilizo sobre todo para el cálculo del interés compuesto, así como en navegación y astronomía para facilitar el cálculo de operaciones tales como multiplicaciones y divisiones grandes, así como el manejo de exponentes y raíces.
Los logaritmos resultaron muy útiles antes del uso de la calculadora en nuestros días para realizar un sinfín de operaciones que de lo contrario hubieran resultado muy tediosas y propensas al error. Para ello se crearon las tablas de logaritmos que ayudaban a realizar estas operaciones.
Actualmente, con el uso de la tecnología el uso de logaritmos para operaciones como una división o una raíz ha caído en desuso para el común de la gente, sin embargo, sigue teniendo gran importancia para la ciencias que necesitan manejar números con gran precisión además de ser operaciones realmente muy complejas para la mayoría de la gente.
Los logaritmos fueron un invento que nos ayudó en el pasado en muchos cálculos que hoy en día son cotidianos y muy fáciles de resolver con la ayuda de una calculadoras o computadora, es por ello que mucha gente desconoce la gran ayuda que prestó en épocas pasadas.

El logaritmo natural o neperiano es uno de esos conceptos que aprendemos sin encontrarle ninguna utilidad práctica más que para los físicos o químicos. La ciencia es excitante, pero las matemáticas detrás de ella pueden frustrarnos. Sin embargo, detrás de cada concepto matemático existe una historia, muchas veces fascinante de cómo una necesidad y una mente creativa pueden encontrar en los números una representación sintetizada de la realidad.
El logaritmo natural, también conocido como logaritmo neperiano en honor del escocés John Napier (cuyo nombre latinizado es Neper) utiliza como base la famosa letra “e” un numero irracional (una división sin fin) cuyo valor aproximado es 2.71821... Los logaritmos pueden ser de cualquier base, sin embargo, los más utilizados es el logaritmo de base 10 también conocido como logaritmo vulgar y el logaritmo natural o neperiano, el cual es más utilizado en ciencias.
Napier fue el creador de la palabra logaritmo (del griego “logos” razón y “arithmos”, numero). Sin embargo, como todo en la ciencia hubo otro hombre quien también trabajó sobre el mismo concepto incluso antes que Napier, este fue el relojero suizo Jobst Bürgi. Sin embargo por cuestión de tiempo, tardó en publicar sus investigaciones hasta el año 1620.
Los logaritmos surgieron por la necesidad de hacer más fáciles operaciones complicadas o tediosas. El concepto de logaritmo como lo conocemos actualmente no surgió de forma inmediata, sino que llevo un proceso de maduración hasta la forma que lo conocemos hoy en día. Se utilizo sobre todo para el cálculo del interés compuesto, así como en navegación y astronomía para facilitar el cálculo de operaciones tales como multiplicaciones y divisiones grandes, así como el manejo de exponentes y raíces.
Los logaritmos resultaron muy útiles antes del uso de la calculadora en nuestros días para realizar un sinfín de operaciones que de lo contrario hubieran resultado muy tediosas y propensas al error. Para ello se crearon las tablas de logaritmos que ayudaban a realizar estas operaciones.
Actualmente, con el uso de la tecnología el uso de logaritmos para operaciones como una división o una raíz ha caído en desuso para el común de la gente, sin embargo, sigue teniendo gran importancia para la ciencias que necesitan manejar números con gran precisión además de ser operaciones realmente muy complejas para la mayoría de la gente.
Los logaritmos fueron un invento que nos ayudó en el pasado en muchos cálculos que hoy en día son cotidianos y muy fáciles de resolver con la ayuda de una calculadoras o computadora, es por ello que mucha gente desconoce la gran ayuda que prestó en épocas pasadas.

NUMEROS HISTORICOS
π (pi)
π (pi) es la relación entre la longitud de una circunferencia y su diámetro, en geometría euclidiana. Es un número irracional y una de las constantes matemáticas más importantes. Se emplea frecuentemente en matemáticas, física e ingeniería. El valor numérico de π, truncado a sus primeras cifras, es el siguiente:
El valor de π se ha obtenido con diversas aproximaciones a lo largo de la historia, siendo una de las constantes matemáticas que más aparece en las ecuaciones de la física, junto con el número e. Por ello, tal vez sea la constante que más pasiones desata entre los matemáticos profesionales y aficionados. La relación entre la circunferencia y su diámetro no es constante en geometrías no euclídeas.
El nombre π
La notación con la letra griega π proviene de la inicial de las palabras de origen griego "περιφέρεια" (periferia) y "περίμετρον" (perímetro) de un círculo,1 notación que fue utilizada primero por William Oughtred (1574-1660), y propuesto su uso por el matemático galés William Jones2 (1675-1749), aunque fue el matemático Leonhard Euler, con su obra «Introducción al cálculo infinitesimal» de 1748, quien la popularizó. Fue conocida anteriormente como constante de Ludolph (en honor al matemático Ludolph van Ceulen) o como constante de Arquímedes (que no se debe confundir con el número de Arquímedes).
Historia del cálculo del valor π
La búsqueda del mayor número de decimales del número π ha supuesto un esfuerzo constante de numerosos científicos a lo largo de la historia. Algunas aproximaciones históricas de π son las siguientes.
Antiguo Egipto
El valor aproximado de π en las antiguas culturas se remonta a la época del escriba egipcio Ahmes en el año 1800 a. C., descrito en el papiro Rhind,3 donde se emplea un valor aproximado de π afirmando que: el área de un círculo es similar a la de un cuadrado, cuyo lado es igual al diámetro del círculo disminuido en 1/9, es decir, igual a 8/9 del diámetro. En notación moderna:
Entre los ocho documentos matemáticos hallados de la antigua cultura egipcia, en dos se habla de círculos. Uno es el papiro Rhind y el otro es el papiro de Moscú. Sólo en el primero se habla del valor aproximado del número π. El investigador Otto Neugebauer, en un anexo de su libro The Exact Sciences in Antiquity,4 describe un método inspirado en los problemas del papiro de Ahmes para averiguar el valor de π, mediante la aproximación del área de un cuadrado de lado 8, a la de un círculo de diámetro 8.
π (pi) es la relación entre la longitud de una circunferencia y su diámetro, en geometría euclidiana. Es un número irracional y una de las constantes matemáticas más importantes. Se emplea frecuentemente en matemáticas, física e ingeniería. El valor numérico de π, truncado a sus primeras cifras, es el siguiente:
El valor de π se ha obtenido con diversas aproximaciones a lo largo de la historia, siendo una de las constantes matemáticas que más aparece en las ecuaciones de la física, junto con el número e. Por ello, tal vez sea la constante que más pasiones desata entre los matemáticos profesionales y aficionados. La relación entre la circunferencia y su diámetro no es constante en geometrías no euclídeas.
El nombre π
La notación con la letra griega π proviene de la inicial de las palabras de origen griego "περιφέρεια" (periferia) y "περίμετρον" (perímetro) de un círculo,1 notación que fue utilizada primero por William Oughtred (1574-1660), y propuesto su uso por el matemático galés William Jones2 (1675-1749), aunque fue el matemático Leonhard Euler, con su obra «Introducción al cálculo infinitesimal» de 1748, quien la popularizó. Fue conocida anteriormente como constante de Ludolph (en honor al matemático Ludolph van Ceulen) o como constante de Arquímedes (que no se debe confundir con el número de Arquímedes).
Historia del cálculo del valor π
La búsqueda del mayor número de decimales del número π ha supuesto un esfuerzo constante de numerosos científicos a lo largo de la historia. Algunas aproximaciones históricas de π son las siguientes.
Antiguo Egipto
El valor aproximado de π en las antiguas culturas se remonta a la época del escriba egipcio Ahmes en el año 1800 a. C., descrito en el papiro Rhind,3 donde se emplea un valor aproximado de π afirmando que: el área de un círculo es similar a la de un cuadrado, cuyo lado es igual al diámetro del círculo disminuido en 1/9, es decir, igual a 8/9 del diámetro. En notación moderna:
Entre los ocho documentos matemáticos hallados de la antigua cultura egipcia, en dos se habla de círculos. Uno es el papiro Rhind y el otro es el papiro de Moscú. Sólo en el primero se habla del valor aproximado del número π. El investigador Otto Neugebauer, en un anexo de su libro The Exact Sciences in Antiquity,4 describe un método inspirado en los problemas del papiro de Ahmes para averiguar el valor de π, mediante la aproximación del área de un cuadrado de lado 8, a la de un círculo de diámetro 8.
HISTORIA DEL NÚMERO AUREO
Hacia 2003 tuve la suerte de entrevistarme varias veces con Amador Rebullida en La Fresneda. En una de nuestras conversaciones me relató que era costumbre hace años (costumbre que ya se ha perdido) que para S. Juan se encendieran hogueras al mismo tiempo en Horta de St. Joan, Calaceite y La Fresneda.
a) el triángulo isósceles es el triángulo aureo (con unos márgenes de error que se pueden observar y son razonables)
b) en consecuencia, la relación entre cualquiera de los lados y la base se aproxima extraordinariamente al número aureo
En efecto:
· si dividimos el lado Calaceite-Horta entre la base Fresneda-Horta, tenemos un valor redondeado a dos decimales de 1,61
El número aureo, redondeado a dos decimales, es 1,62 ¿Casualidad?
¿Qué es el número aúreo?
Número áureo
El número aureo o de oro (también llamado número dorado, sección áurea, razón áurea, razón dorada, media áurea, proporción áurea y divina proporción) representado por la letra griega f (fi) (en honor al escultor griego Fidias), es el número irracional:

Se trata de un número algebraico que posee muchas propiedades interesantes y que fue descubierto en la antigüedad, no como “unidad” sino como relación o proporción. Esta proporción se encuentra tanto en algunas figuras geométricas como en la naturaleza en elementos tales como caracolas, nervaduras de las hojas de algunos árboles, el grosor de las ramas, etc.
Asímismo, se atribuye un carácter estético especial a los objetos que siguen la razón áurea, así como una importancia mística. A lo largo de la historia, se le ha atribuido importancia en diversas obras de arquitectura y otras artes, aunque algunos de estos casos han sido objetables para las matemáticas y la arqueología. (...)
Historia del número áureo
Existen numerosos textos que sugieren que el número áureo se encuentra como proporción en ciertas estelas Babilonias y Asirias de alrededor de 2000 a. C. Sin embargo no existe documentación histórica que indique que el número áureo fue usado conscientemente por los arquitectos o artistas en la construcción de las estelas. También es importante notar que cuando se mide una estructura complicada es fácil obtener resultados curiosos si se tienen muchas medidas disponibles. Además para que se pueda considerar que el número áureo está presente, las medidas deben tomarse desde puntos relativamente obvios del objeto y este no es el caso de los elaborados teoremas que defienden la presencia del número áureo. Por todas estas razones Mario Livio concluye que es muy improbable que los babilonios hayan descubierto el número áureo.
El primero en hacer un estudio formal sobre el número áureo fue Euclides (c. 300-265 a. C.), quién lo definió de la siguiente manera:
"Se dice que una línea recta está dividida en el extremo y su proporcional cuando la línea entera es al segmento mayor como el mayor es al menor."
Euclides en Los Elementos.
Euclices demostró también que este número no puede ser descrito como la razón de dos números enteros, es decir es irracional.
Platón (c. 428-347 a. C.) vivió antes de que Euclides estudiara el número áureo, sin embargo, a veces el desarrollo de teoremas relacionados, él, debido a eso Proclo escribió:
"Eudoxo... multiplicó el número de teoremas relativos a la sección a los que Platón dio origen."
Proclo en Un comentario sobre el Primer Libro de los Elementos de Euclides.
Aquí a menudo se interpretó la palabra sección (t?µ?) como la sección áurea. Sin embargo a partir del siglo XIX esta interpretación ha sido motivo de gran controversia y muchos investigadores han llegado a la conclusión de que la palabra sección no tuvo nada que ver con el número áureo. No obstante, Platón consideró que los números irracionales, descubiertos por los pitagóricos, eran de particular importancia y la llave a la física del cosmos. Esta opinión tuvo una gran influencia en muchos filósofos y matemáticos posteriores, en particular los neoplatónicos. (...)
En 1509 el matemático y teólogo Luca Pacioli publica su libro De Divina Proportione (La Proporción Divina), en el que plantea cinco razones por las que considera apropiado considerar divino al Número áureo:
La unicidad; Pacioli compara el valor único del número áureo con la unicidad de Dios.
El hecho de que esté definido por tres segmentos de recta, Pacioli lo asocia con la Trinidad.
La inconmesurabilidad; para Pacioli la inconmesurabilidad del número áureo, y la inconmesurabilidad de Dios son equivalentes.
La Autosimilaridad asociada al número áureo; Pacioli la compara con la omnipresencia e invariabilidad de Dios.
Según Pacioli, de la misma manera en que Dios dio ser ser al Universo a través de la quinta esencia, representada por el dodecaedro; el número áureo dio ser al dodecaedro.
En 1525, Alberto Durero publica Instrucción sobre la medida con regla y compás de figuras planas y sólidas donde describe cómo trazar con regla y compás la espiral basada en la sección áurea, que se conoce como “espiral de Durero”.
El astrónomo Johannes Kepler (1571-1630), desarrolló un modelo Platónico del Sistema Solar utilizando los sólidos platónicos, y se refirió al número áureo en términos grandiosos
“La geometría tiene dos grandes tesoros: uno es el teorema de Pitágoras; el otro, la división de una línea entre el extremo y su proporcional. El primero lo podemos comparar a una medida de oro; el segundo lo debemos denominar una joya preciosa”
Johannes Kepler en Mysterium Cosmographicum (El Misterio Cósmico).
El primer uso conocido del adjetivo áureo, dorado, o de oro, para referise a este número lo hace el matemático alemán Martin Ohm, hermano del célebre físico Georg Simon Ohm, en la segunda edición de 1835 de su libro Die Reine Elementar Matematik (Las Matemáticas Puras Elementales). Ohm escribe en una nota al pie:
"Uno también acostumbra llamar a esta división de una línea arbitraria en dos partes como éstas la sección dorada."
Martin Ohm en Die Reine Elementar Matematik (Las Matemáticas Puras Elementales).
(...)
El número áureo en la geometría
El número áureo y la sección áurea están presentes en todos los objetos geométricos regulares o semiregulares en los que haya simetría pentagonal, pentágonos o aparezca de alguna manera la raíz cuadrada de cinco.
* Relaciones entre las partes del pentágono.
* Relaciones entre las partes del pentágono estrellado, pentáculo o pentagrama.
* Relaciones entre las partes del decágono.
* Relaciones entre las partes del dodecaedro y del icosaedro.
(...)
En el pentagrama
Pentagrama que ilustra algunas de las razones áureas: los segmentos rojo y azul, azul y verde, verde y morado.
El número áureo tiene un papel muy importante en los pentágonos regulares y en los pentagramas. Cada intersección de partes de un segmento, intersecta a otro segmento en una razón áurea.
El pentagrama incluye diez triángulos isóceles: cinco acutángulos y cinco obtusángulos. En ambos, la razón de lado mayor y el menor es f. Estos triángulos se conocen como los triángulos áureos.
Teniendo en cuenta la gran simetría de este símbolo se observa que dentro del pentágono interior es posible dibujar una nueva estrella, con una recursividad hasta el infinito. Del mismo modo, es posible dibujar un pentágono por el exterior, que sería a su vez el pentágono interior de una estrella más grande. Al medir la longitud total de una de las cinco líneas del pentáculo interior, resulta igual a la longitud de cualquiera de los brazos de la estrella mayor, o sea F. Por lo tanto el número de veces en que aprarece el número áureo en el pentagrama es infinito al anidar infinitos pentagramas.(...)
El número áureo en la Naturaleza
Concha de nautilus en espiral logarítmica
En la naturaleza, hay muchos elementos relacionados con la sección áurea:
No hay simetría pentagonal ni pentágonos en la materia inanimada. El pentágono surge únicamente en los seres vivos, ningún cristal, por ejemplo, tiene forma pentagonal. (...)
* El cociente de dos términos sucesivos de la Sucesión de Fibonacci tiende a la sección áurea o al número áureo si la fracción resultante es propia o impropia, respectivamente. Lo mismo sucede con toda sucesión recurrente de orden dos, según demostraron Barr y Schooling en la revista The Field del 14 de diciembre de 1912.
* La relación entre la cantidad de abejas macho y abejas hembra en un panal.
* La disposición de los pétalos de las flores (el papel del número áureo en la botánica recibe el nombre de Ley de Ludwig).
* La distribución de las hojas en un tallo.
* La relación entre las nervaduras de las hojas de los árboles
* La relación entre el grosor de las ramas principales y el tronco, o entre las ramas principales y las secundarias (el grosor de una equivale a F tomando como unidad la rama superior).
* La distancia entre las espirales de una piña.
* La relación entre la distancia entre las espiras del interior espiralado de cualquier caracol (no sólo del nautilus) Hay por lo menos tres espirales logarítmicas en las que se puede encontrar de alguna manera al número áureo. La primera de ellas se caracteriza por la relación constante igual al número áureo entre los radiovectores de puntos situados en dos evolutas consecutivas en una misma dirección y sentido. Las conchas del Fusus antiquus, del Murex, de Scalaria pretiosa, de Facelaria y de Solarium trochleare, entre otras, siguen este tipo de espiral de crecimiento. Se debe entender que en toda consideración natural, aunque involucre a las ciencias consideradas más matemáticamente desarrolladas, como la Física, ninguna relación o constante que tenga un número infinito de decimales puede llegar hasta el límite matemático, porque en esa escala no existiría ningún objeto físico. La partícula elemental más diminuta que se pueda imaginar es infinitamente más grande que un punto en una recta. Las leyes observadas y descriptas matemáticamente en los organismos las cumplen transgrediéndolas orgánicamente. [
El número áureo en la religión
Un estudio realizado por la SARU (Science and religion united = ciencia y religión unidas) en noviembre del año 2005, analizó meticulosamente el "Evangelio Prohibido de Judas" descubierto a principios del año 2000 (aquel que afirma que en realidad Jesús le pidio a Judas que lo traicione), . Entre otros hallazgos, fue notorio el hecho de que se detallaran las medidas de la cruz en la cual Jesucristo fue crucificado, y más sorprendentemente, una de sus características: el trozo de madera más largo de esta medía 3,23 m aproximadamente; mientras que el trozo más corto tenía una longitud aproximada de 2m. Lo curioso fue que notaron que al dividir la longitud del trozo mayor por la del menor se obtiene (usted mismo puede comprobarlo) 1,615, que es el valor aproximado de F. También notaron que si tomaran como base al trozo más largo de la cruz, y como altura al más corto, estarían en presencia de un rectángulo aúreo.
Otro estudio de la SARU, en este caso sobre el Santo Sudario (la tela en que se cree que Jesús fue envuelto en su sepulcro), en el que se presentan marcas y traumas físicos propios de la crucifixión; demuestra que las marcas alrededor del cráneo que, según se cree, fueron causadas por la corona de espinas, se presentan en forma de espiral logarítmico, y consecuentemente sus espinas siguen la sucesión de Fibonacci.
Evidentemente, es por algo que se conoce también a Phi como la Proporción Divina.
El número áureo en el ser humano
La Anatomía de los humanos se basa en una relación F estadística y aproximada, así vemos que:
* La relación entre la altura de un ser humano y la altura de su ombligo.
* La relación entre la distancia del hombro a los dedos y la distancia del codo a los dedos.
* La relación entre la altura de la cadera y la altura de la rodilla.
* La relación entre el primer hueso de los dedos (metacarpiano) y la primera falange, o entre la primera y la segunda, o entre la segunda y la tercera, si dividimos todo es phi.
* La relación entre el diámetro de la boca y el de la nariz
* Es phi la relación entre el diámetro externo de los ojos y la línea inter-pupilar
* Cuando la tráquea se divide en sus bronquios, si se mide el diámetro de los bronquios por el de la tráquea se obtiene phi, o el de la aorta con sus dos ramas terminales (ilíacas primitivas).
El número áureo en el Arte
* Relaciones en la forma de la Gran Pirámide de Gizeh. La afirmación de Herodoto de que el cuadrado de la altura es igual a la superficie de una cara es posible únicamente si la semi-sección meridiana de la pirámide es proporcional al triángulo rectángulo  , donde 1 representa proporcionalmente a la mitad de la base, la raíz cuadrada del número áureo a la altura hasta el vértice inexistente y el número áureo o hipotenusa del triángulo a la apotema de la Gran Pirámide. Esta tesis ha sido defendida por los matemáticos Jarolimek, K. Kleppisch y W. A. Price (ver referencias), cuenta con el testimonio histórico de Herodoto y resulta teóricamente con sentido, aunque una construcción de semejante tamaño deba contener errores inevitables a toda obra arquitectónica y a la misma naturaleza de la tecnología humana, que en la práctica puede manejar únicamente números racionales. Los demás investigadores famosos se inclinan por la hipótesis de que los constructores intentaron una cuadratura del círculo, pues la raíz cuadrada del número áureo se aproxima mucho al cociente de 4 sobre p. Pero una construcción tal, aunque se conociera p con una aproximación grande, carecería completamente de sentido matemático. No obstante, en base a mediciones no es posible elegir entre una u otra pues la diferencia sobre el monumento real no es mayor a 14,2 cm y esta pequeña variación queda enmascarada por las incertidumbres de las medidas, los errores constructivos y, principalmente, porque la pirámide perdió el revestimiento en manos de los primeros constructores de El Cairo. Para que esto quede más claro, una precisión del 1 por mil en una base de 230 metros equivale a 23 centímetros y en la altura está en el orden de la diferencia real que debería existir entre ambas posibilidades.
, donde 1 representa proporcionalmente a la mitad de la base, la raíz cuadrada del número áureo a la altura hasta el vértice inexistente y el número áureo o hipotenusa del triángulo a la apotema de la Gran Pirámide. Esta tesis ha sido defendida por los matemáticos Jarolimek, K. Kleppisch y W. A. Price (ver referencias), cuenta con el testimonio histórico de Herodoto y resulta teóricamente con sentido, aunque una construcción de semejante tamaño deba contener errores inevitables a toda obra arquitectónica y a la misma naturaleza de la tecnología humana, que en la práctica puede manejar únicamente números racionales. Los demás investigadores famosos se inclinan por la hipótesis de que los constructores intentaron una cuadratura del círculo, pues la raíz cuadrada del número áureo se aproxima mucho al cociente de 4 sobre p. Pero una construcción tal, aunque se conociera p con una aproximación grande, carecería completamente de sentido matemático. No obstante, en base a mediciones no es posible elegir entre una u otra pues la diferencia sobre el monumento real no es mayor a 14,2 cm y esta pequeña variación queda enmascarada por las incertidumbres de las medidas, los errores constructivos y, principalmente, porque la pirámide perdió el revestimiento en manos de los primeros constructores de El Cairo. Para que esto quede más claro, una precisión del 1 por mil en una base de 230 metros equivale a 23 centímetros y en la altura está en el orden de la diferencia real que debería existir entre ambas posibilidades.
 , donde 1 representa proporcionalmente a la mitad de la base, la raíz cuadrada del número áureo a la altura hasta el vértice inexistente y el número áureo o hipotenusa del triángulo a la apotema de la Gran Pirámide. Esta tesis ha sido defendida por los matemáticos Jarolimek, K. Kleppisch y W. A. Price (ver referencias), cuenta con el testimonio histórico de Herodoto y resulta teóricamente con sentido, aunque una construcción de semejante tamaño deba contener errores inevitables a toda obra arquitectónica y a la misma naturaleza de la tecnología humana, que en la práctica puede manejar únicamente números racionales. Los demás investigadores famosos se inclinan por la hipótesis de que los constructores intentaron una cuadratura del círculo, pues la raíz cuadrada del número áureo se aproxima mucho al cociente de 4 sobre p. Pero una construcción tal, aunque se conociera p con una aproximación grande, carecería completamente de sentido matemático. No obstante, en base a mediciones no es posible elegir entre una u otra pues la diferencia sobre el monumento real no es mayor a 14,2 cm y esta pequeña variación queda enmascarada por las incertidumbres de las medidas, los errores constructivos y, principalmente, porque la pirámide perdió el revestimiento en manos de los primeros constructores de El Cairo. Para que esto quede más claro, una precisión del 1 por mil en una base de 230 metros equivale a 23 centímetros y en la altura está en el orden de la diferencia real que debería existir entre ambas posibilidades.
, donde 1 representa proporcionalmente a la mitad de la base, la raíz cuadrada del número áureo a la altura hasta el vértice inexistente y el número áureo o hipotenusa del triángulo a la apotema de la Gran Pirámide. Esta tesis ha sido defendida por los matemáticos Jarolimek, K. Kleppisch y W. A. Price (ver referencias), cuenta con el testimonio histórico de Herodoto y resulta teóricamente con sentido, aunque una construcción de semejante tamaño deba contener errores inevitables a toda obra arquitectónica y a la misma naturaleza de la tecnología humana, que en la práctica puede manejar únicamente números racionales. Los demás investigadores famosos se inclinan por la hipótesis de que los constructores intentaron una cuadratura del círculo, pues la raíz cuadrada del número áureo se aproxima mucho al cociente de 4 sobre p. Pero una construcción tal, aunque se conociera p con una aproximación grande, carecería completamente de sentido matemático. No obstante, en base a mediciones no es posible elegir entre una u otra pues la diferencia sobre el monumento real no es mayor a 14,2 cm y esta pequeña variación queda enmascarada por las incertidumbres de las medidas, los errores constructivos y, principalmente, porque la pirámide perdió el revestimiento en manos de los primeros constructores de El Cairo. Para que esto quede más claro, una precisión del 1 por mil en una base de 230 metros equivale a 23 centímetros y en la altura está en el orden de la diferencia real que debería existir entre ambas posibilidades.
* La relación entre las partes, el techo y las columnas del Partenón, en Atenas (s. V a. C.). Durante el primer cuarto del siglo XX, Jay Hambidge, de la Universidad de Yale, se inspiró en un pasaje del Theeteto de Platón para estudiar las proporciones relativas de las superficies, algo muy natural cuando se trata de obras arquitectónicas. Dos rectángulos no semejantes se distinguen entre sí por el cociente de su lado mayor por el menor, número que basta para caracterizar a estas figuras y que denominó módulo del rectángulo. Un cuadrado tiene módulo 1 y el doble cuadrado módulo 2. Aquellos rectángulos cuyos módulos son números enteros o racionales fueron denominados "estáticos" y los que poseen módulos irracionales euclidianos, o sea, expresables algebraicamente como raíces de ecuaciones cuadráticas o reducibles a ellas, "dinámicos". El doble cuadrado es a la vez estático y dinámico, pues 2 es la raíz cuadrada de 4. Un ejemplo de rectángulo dinámico elemental es aquel que tiene por lado mayor a la raíz cuadrada de 5 y por lado menor a la unidad, siendo su módulo la raíz cuadrada de 5. Posteriormente Hambidge estudió a los monumentos y templos griegos y llegó a encuadrar el frontón del Partenón en un rectángulo de módulo  . Por medio de cuatro diagonales suministra las principales proporciones verticales y horizontales. Este rectángulo es descompuesto en seis de módulo
. Por medio de cuatro diagonales suministra las principales proporciones verticales y horizontales. Este rectángulo es descompuesto en seis de módulo  y cuatro cuadrados. Como dato adicional para indicar la complejidad del tratamiento del edificio se tiene que en 1837 fueron descubiertas correcciones ópticas en el Partenón. El templo tiene tres vistas principales y si sus columnas estuvieran efectivamente a plomo, todas sus líneas fuesen paralelas y perfectamente rectas y los ángulos rectos fueran exactos, por las propiedades de la visión humana el conjunto se vería más ancho arriba que en la base, sus columnas se percibirían inclinadas hacia afuera y la línea que fundamenta el techo sobre las columnas se vería como una especie de catenaria, con los extremos del edificio aparentemente más altos que el centro. Los constructores hicieron la construcción compensando estos efectos de ilusión óptica inclinando o curvando en sentido inverso a los elementos involucrados. Así las columnas exteriores,en ambos lados del frente, están inclinadas hacia adentro en un ángulo de 2,65 segundos de arco, mientras que las que están en el medio tienen una inclinación de 2,61 segundos de arco. La línea que formarían los dinteles entre columnas y que constituye la base del triángulo que corona el edificio, en realidad es un ángulo de 2,64 segundos de arco con el vértice más elevado que los extremos. De esta forma, y con otras correcciones que no se mencionan aquí, se logra que cualquier observador que se sitúe en los tres puntos principales de vista vea todo el conjunto paralelo, uniforme y recto.
y cuatro cuadrados. Como dato adicional para indicar la complejidad del tratamiento del edificio se tiene que en 1837 fueron descubiertas correcciones ópticas en el Partenón. El templo tiene tres vistas principales y si sus columnas estuvieran efectivamente a plomo, todas sus líneas fuesen paralelas y perfectamente rectas y los ángulos rectos fueran exactos, por las propiedades de la visión humana el conjunto se vería más ancho arriba que en la base, sus columnas se percibirían inclinadas hacia afuera y la línea que fundamenta el techo sobre las columnas se vería como una especie de catenaria, con los extremos del edificio aparentemente más altos que el centro. Los constructores hicieron la construcción compensando estos efectos de ilusión óptica inclinando o curvando en sentido inverso a los elementos involucrados. Así las columnas exteriores,en ambos lados del frente, están inclinadas hacia adentro en un ángulo de 2,65 segundos de arco, mientras que las que están en el medio tienen una inclinación de 2,61 segundos de arco. La línea que formarían los dinteles entre columnas y que constituye la base del triángulo que corona el edificio, en realidad es un ángulo de 2,64 segundos de arco con el vértice más elevado que los extremos. De esta forma, y con otras correcciones que no se mencionan aquí, se logra que cualquier observador que se sitúe en los tres puntos principales de vista vea todo el conjunto paralelo, uniforme y recto.
 . Por medio de cuatro diagonales suministra las principales proporciones verticales y horizontales. Este rectángulo es descompuesto en seis de módulo
. Por medio de cuatro diagonales suministra las principales proporciones verticales y horizontales. Este rectángulo es descompuesto en seis de módulo
* En el cuadro Leda atómica de Salvador Dalí, hecho en colaboración con el matemático rumano Matila Ghyka.
* En los violines, la ubicación de las efes (los “oídos”, u orificios en la tapa) se relaciona con el número áureo.
* El número áureo aparece en las relaciones entre altura y ancho de los objetos y personas que aparecen en las obras de Miguel Ángel, Durero y Da Vinci, entre otros.
* Las relaciones entre articulaciones en el hombre de Vitruvio y en otras obras de Leonardo da Vinci.
* En las estructuras formales de las sonatas de Mozart, en la Quinta Sinfonía de Beethoven, en obras de Schubert y Debussý (estos compositores probablemente compusieron estas relaciones de manera inconsciente, basándose en equilibrios de masas sonoras). (...)
* Arte Póvera, movimiento artístico italiano de los años 1960, muchas de cuyas obras se basan en esta sucesión.
* En la cinta de Darren Aronofsky Pi, el orden del caos el personaje central, Max Cohen, explica la relación que hay entre los números de Fibonacci y la sección áurea, aunque denominándola incorrectamente como Theta (?) en vez de Phi (F).
El número áureo en la Música
Es necesario aclarar que cuando se menciona al número áureo en una realización artística de cualquier naturaleza no se está haciendo mención al número áureo de los matemáticos, un irracional con infinitos decimales, sino a una aproximación racional adecuada a las circunstancias o a un dibujo hecho con regla no graduada de un solo borde y longitud indefinida y un compás de abertura fija o variable. Generalmente se utilizan cocientes de números pertenecientes a la sucesión de Fibonacci que dan valores aproximados, alternativamente por defecto o por exceso, según la necesidad o la sensibilidad humana y hasta la capacidad de separación tonal de cada instrumento. Un violín, por ejemplo, puede separar hasta un tercio de tono. El oído humano sano y entrenado distingue hasta trescientos sonidos por octava. Como un ejemplo conocido y no discutido tenemos a la escala atemperada o templada. Esta es una escala logarítmica. Se creó muy poco tiempo después de que los logaritmos pasaran al patrimonio de la matemática. La octava atemperada está basada en  . Este número irracional tiene infinitos decimales, pero la afinación se hace redondeando las cifras de las frecuencias a uno o dos decimales. De cualquier manera, el error tonal total cometido no es superior al doceavo de tono y el oído humano no lo nota. La uniformidad de la separación de las notas y la coincidencia de bemoles y sostenidos permite comenzar una melodía por cualquier nota sin que se produzcan las desagradables disonancias de la escala diatónica y la escala física. De la misma manera se actúa con la distribución de tiempos o la altura de los tonos usando el número áureo; con una aproximación racional que resulte práctica. Existen numerosos estudios al respecto, principalmente de la Universidad de Cambridge.
. Este número irracional tiene infinitos decimales, pero la afinación se hace redondeando las cifras de las frecuencias a uno o dos decimales. De cualquier manera, el error tonal total cometido no es superior al doceavo de tono y el oído humano no lo nota. La uniformidad de la separación de las notas y la coincidencia de bemoles y sostenidos permite comenzar una melodía por cualquier nota sin que se produzcan las desagradables disonancias de la escala diatónica y la escala física. De la misma manera se actúa con la distribución de tiempos o la altura de los tonos usando el número áureo; con una aproximación racional que resulte práctica. Existen numerosos estudios al respecto, principalmente de la Universidad de Cambridge.
Autores como Bártok, Messiaen y Stockhausen, entre otros, compusieron obras cuyas unidades formales se relacionan (a propósito) con la sección áurea.
El compositor mexicano Silvestre Revueltas (1899-1945) utilizó también el número áureo en su obra Alcancías, para organizar las partes (unidades formales).
El grupo de rock progresivo norteamericano Tool, en su disco Lateralus (2001) hacen múltiples referencias al número áureo y a la secuencia Fibonacci, sobre todo en la canción que da nombre al disco, pues los versos de la misma están cantados de forma que el número de sílabas pronunciadas en cada uno van componiendo dicha secuencia. Además la voz entra en el minuto 1:37, que pasado al sistema decimal coincide muy aproximadamente con el número áureo.
Zeysing notó la presencia de los números 3, 5, 8 y 13, de la Sucesión de Fibonacci, en el cálculo de los intervalos aferentes a los dos tipos de acordes perfectos. Los dos tonos del acorde mayor final, mi y do por ejemplo (la sexta menor o tercia mayor invertida en do mayor), están entre sí en la razón cinco octavos. Los dos tonos del acorde menor final, por ejemplo, mi bemol y do (sexta mayor o tercia transpuesta en do menor) dan la razón tres quintos.[
DIA DEL PADRE
Día del Padre :
"La señora Joan B. Dodd, de Washington, fue la que propuso la idea del "Día del Padre" en 1909. La señora Dodd quería que existiera un día especial que honrara a su padre William Dood. Willian Dodd, veterano de guerra civil, se convirtió en viudo cuando su esposa (la madre de la señora Dodd) murió en parto con su sexto niño.
Fue en una granja rural en el estado de Washington en que el Sr. Dodd se hizo cargo para educar a seis niños. Fue después en que la señora Dodd se dio cuenta que su padre había sido un verdadero ejemplo al criar a todos sus hijos con verdadera educación y valores. El primer día del padre se celebro el 19 de junio de 1910 con Spokane Washington.
En ese mismo tiempo en varias ciudades a través de Estados Unidos la gente comenzaba a celebrar "El Día del Padre". En 1924 el presidente Calvin Coolidge hizo el día del padre como una celebración nacional. Finalmente en 1966 el presidente Lyndon Johnson firmó una proclamación presidencial que declaraba el 3er domingo de junio como día del padre.


RAZONES TRIGONOMETRICAS
TRIGONOMETRÍA.
Ángulo. Porción de plano comprendida entre dos rectas que se cruzan
.

Medida de ángulos.
- Grados sexagesimales (DEG) 1º=60'=3600'' La circunferencia está dividida en 360º
- Radianes (RAD) 360º=2·pi radianes.
Razones trigonométricas. Dada una circunferencia de radio r, si tomamos un arco AP, donde A es un punto del semieje positivo de las x y P(x,y), el punto del extremo, se definen las razones trigonométricas del ángulo en la forma:
AP, donde A es un punto del semieje positivo de las x y P(x,y), el punto del extremo, se definen las razones trigonométricas del ángulo en la forma:
 AP, donde A es un punto del semieje positivo de las x y P(x,y), el punto del extremo, se definen las razones trigonométricas del ángulo en la forma:
AP, donde A es un punto del semieje positivo de las x y P(x,y), el punto del extremo, se definen las razones trigonométricas del ángulo en la forma:- Seno sen a = ordenada / radio = y / r
- Coseno cos a = abscisa / radio = x / r
- Tangente tg a = seno / coseno = ordenada / abscisa = y / x
- Cotangente cotg a = coseno / seno = abscisa / ordenada = x / y
- Secante sec a = 1 / coseno = 1 / (x / r) = r / x
- Cosecante cosec a = 1 / seno = 1 / (y / r) = r / y
Signo de las razones. En cada cuadrante, dependiendo del signo de las abscisas y ordenadas, las razones presentan los siguientes signos:

Ángulos notables.
- 30º Para determinar sus razones tenemos en cuenta que se forma un triángulo equilátero:
 sen 30º = y/r= (r/2) / r = 1/2
sen 30º = y/r= (r/2) / r = 1/2
cos 30º = x/r= 3½ / 2
r2=x2+(r/2)2=x2+r2/4 x=(3r2/4)½=r3½/2
tg 30 º=(1/2)/(3½/2)= 3½ / 3
- 60º Formamos el triángulo equilátero de la figura:
 sen 60º= y/r= (r 3½ / 2)/r= 3½ / 2
sen 60º= y/r= (r 3½ / 2)/r= 3½ / 2
r2 = y2 + ( r/2)2
y = ( r2-r2/4)½ = ( 3 r2 / 4 )½ = r 3½ / 2
cos 60º= (r/2)/r = 1 / 2
tg 60º = (3½ / 2)/(1/2) = 3½
- 45º La x y la y son iguales, por lo que se forma un triángulo isósceles:
 sen 45º = y/r = 2½ / 2
sen 45º = y/r = 2½ / 2
r2 = x2 + y2 = 2 y2
y=(r2/2)½=r(2½)/2
cos 45º= x/r = y = 2½ / 2
tg 45º = sen 45º / cos 45º = 1
Relaciones entre las razones trigonométricas.
1.- Teorema fundamental.
 sen a = y / r de donde y = r sen a
sen a = y / r de donde y = r sen a
cos a = x / r de donde x = r cos a
como según Pitágoras: x2+y2=r2 tenemos que r2cos2a + r2sen2a=r2
es decir: cos2a + sen2a = 1
2.- Dividiendo el teorema fundamental entre sen2:
1 + cos2a / sen2a = 1/ sen2a
1 + cotg2a = cosec2a
3.- Dividiendo el teorema fundamental entre cos2:
tg2a+1= 1 / cos2a
1 + tg2a = sec2a
Relaciones entre las razones trrigonométricas de algunos ángulos.
1. ángulos suplementarios. Teniendo en cuenta la definición de cada razón trigonométrica, se deduce:
Teniendo en cuenta la definición de cada razón trigonométrica, se deduce:
 Teniendo en cuenta la definición de cada razón trigonométrica, se deduce:
Teniendo en cuenta la definición de cada razón trigonométrica, se deduce:
sen a = sen b cos a = - cos b tg a = - tg b
2. ángulos complementarios.
 Observamos que y'=x y que x'=y
Observamos que y'=x y que x'=y
sen b = sen (90-a) = y'/r = x/r = cos a
cos b = cos (90-a) = x'/r = y / r = sen a
tg b = cotg a
3. ángulos que difieren en 180º
 sen b = sen (180+a) = - sen a
sen b = sen (180+a) = - sen a
cos b = cos (180+a) = - cos a
tg b = sen b / cos b = - sen a / - cos a = tg a
4.- ángulos opuestos.
 sen b = y´/r = - y/r = -sen a
sen b = y´/r = - y/r = -sen a
cos b = x´/r = x/r = - y/r = cos a
tg b = sen b / cos b = - sen a / cos a = - tg a
Representación de las razones trigonométricas sobre la circunferencia goniométrica.
Se denomina circunferencia goniométrica a la que tiene de radio la unidad.
En esta circunferencia: sen a = y / r = y
cos a = x / r = x
tg a = y / x = y' / x' = y' ya que x'=1
cotg a = x / y = x' / y' = x' ya que y'=1
sec a = 1/cos a = 1/(x/r)= r / x = r' / x' = r' ya que x'=1
cosec a = 1/sen a = 1/(y/r)= r / y = r' / y' = r' ya que y'=1


TEOREMAS DE ADICIÓN
1.- ADICIÓN DE ÁNGULOS. Suponemos circunferencia goniométrica (R=1)
a) Coseno de la suma.
 cos(a+b)=OC/OB=OC=OD-CD=OD-BE=OAcosa-ABsena=
cos(a+b)=OC/OB=OC=OD-CD=OD-BE=OAcosa-ABsena=
=OBcosbcosa-OBsenbsena=cosacosb-senasenb
b) Coseno de la diferencia. En la expresión del coseno de la suma sustituímos b por -b
cos(a-b)=cos[a+(-b)]=cosacos(-b)-senasen(-b)=cosacosb-sena(-senb)=cosacosb+senasenb
c) Seno de la suma.
sen(a+b)=-cos[a+(b+90)]=-[cosacos(b+90)-senasen(b+90)]=-[cosa(-senb)-senacosb]=
=senacosb+cosasenb
d) Seno de la diferencia.
sen(a-b)=senacos(-b)+cosasen(-b)=senacosb-cosasenb
e) Tangente de la suma.
tg(a+b)=sen(a+b)/cos(a+b)=(senacosb+cosasenb)/(cosacosb-senasenb)=(tga+tgb)/(1-tgatgb)
f) Tangente de la diferencia.
tg(a-b)=sen(a-b)/cos(a-b)=(senacosb-cosasenb)/(cosacosb+senasenb)=(tga-tgb)/(1+tgatgb)
g) Coseno del ángulo doble. Hacemos b=a en la expresión del coseno de la suma
cos(a+b)=cosacosb-senasenb=cos2a-sen2a Es decir: cos(2a)=cos2a-sen2a
h) Seno del ángulo doble. Hacemos b=a en la expresión del coseno de la suma
sen(a+b)=senacosb+cosasenb=senacosa+cosasena=2senacosa Luego: sen(2a)=2senacosa
i) Tangente del ángulo doble.
tg(a+b)=(tga+tga)/(1-tgatga)=2tga/(1-tg2a)
j) y k) Coseno y seno del ángulo mitad.
cos(2a)=cos2a-sen2a Si hacemos a=a/2 tenemos: cosa=cos2(a/2)-sen2(a/2)
y como según Pitágoras: 1=cos2(a/2)+sen2(a/2)
sumando ambas expresiones: 1+cosa=2cos2(a/2) de donde: cos(a/2)=[(1+cosa)/2]½
restándolas: 1-cosa=2sen2(a/2) de donde: sen(a/2)=[(1-cosa)/2]½
l) Tangente del ángulo mitad.
tg(a/2)=sen(a/2)/cos(a/2)=[(1-cosa)/2]½ / [(1+cosa)/2]½=[(1-cosa)/(1+cosa)]½
2.- ADICIÓN DE RAZONES TRIGONOMÉTRICAS.
m) Suma de cosenos.
cos(p+q)=cos p · cos q-sen p·sen q
cos(p-q)=cos p·cos q+sen p·sen q Sumando: cos(p+q)+cos(p-q)=2·cos p·cos q
Si llamamos: p+q=A y p-q=B tenemos que: p=A-q A-2q=B q=(A-B)/2
p=A-(A-B)/2=(A+B)/2
sustituyendo: cos A + cos B = 2·cos[(A + B) / 2] ·[cos (A-B) / 2]
n) Diferencia de cosenos:
cos(p+q)-cos(p-q) = -2·sen p· sen q
cos A - cos B = - 2·sen[ (A+B) /2 ]·sen[ (A-B) / 2]
ñ) Suma de senos.
sen(p+q)=sen p·cos q+cos p·sen q
sen(p-q)=sen p·cos q-cos p·sen q
sen(p+q)+sen(p-q)=2·sen p·cos q
sen A + sen B = 2·sen[ (A+B) / 2]·cos [(A-B) / 2]
o) Diferencia de senos.
sen(p+q)-sen(p-q)=2·cos p·sen q
sen A - sen B = 2·cos[(A+B) / 2]·sen[ (A- B) / 2]
Suscribirse a:
Comentarios (Atom)
![\gamma = \lim_{n \rightarrow \infty } \left[
\sum_{k=1}^n \frac{1}{k} - \ln(n)\right]=\int_1^\infty\left({1\over\lfloor x\rfloor}-{1\over x}\right)\,dx](http://upload.wikimedia.org/math/1/0/5/1052749ba2986f314a37315f1e0e6507.png)

![\gamma = \sum_{k=1}^\infty \left[ \frac{1}{k} - \ln \left( 1 + \frac{1}{k} \right) \right]](http://upload.wikimedia.org/math/8/9/2/89211028b40ce9518421d03a40474722.png)

![\gamma = \lim_{n \to \infty} \left [ n - \Gamma \left ( \frac{1}{n} \right ) \right ]](http://upload.wikimedia.org/math/9/c/6/9c638e815f0b7097504a14c3b11b8242.png)
![-\gamma = \lim_{n \to \infty} \left [ \frac{ \Gamma(\frac{1}{n}) \Gamma(n+1)\, n^{1+{1 \over n}}}{\Gamma(2+n+\frac{1}{n})} - \frac{n^2}{n+1} \right ]](http://upload.wikimedia.org/math/5/6/6/566f6e07cfe5a5d190a810ac464d9745.png)
![-\gamma = \lim_{n \to \infty} \left [n^{2+{1 \over n}} \, \Beta \left( 1 + \frac{1}{n},\, n + 1 \right ) - \frac{n^2}{n+1} \right ]](http://upload.wikimedia.org/math/7/e/3/7e31a0734e46433412820fdc04d4d120.png)
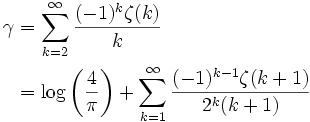
![\begin{align}
\gamma & = \frac{3}{2}- \log 2 - \sum_{k=2}^\infty (-1)^k\,\frac{k-1}{k} [\zeta(k)-1]\\
{} & = \lim_{n \to \infty} \left [ \frac{2\,n-1}{2\,n} - \log\,n + \sum_{k=2}^n \left ( \frac{1}{k} - \frac{\zeta(1-k)}{n^k} \right ) \right ]\\
{} & = \lim_{n \to \infty} \left [ \frac{2^n}{e^{2^n}} \sum_{k=0}^\infty \frac{2^{k \,n}}{(k+1)!} \sum_{t=0}^k \frac{1}{t+1} - n\, \log 2+ \mathcal{O} \left ( \frac{1}{2^n\,e^{2^n}} \right ) \right ]
\end{align}](http://upload.wikimedia.org/math/5/d/2/5d210739d9779cf0ca8f4658c6dd15ef.png)